LLM Architecture Series – Lesson 14 of 20. At this point attention and MLP layers are doing heavy work. Residual connections make sure information can flow easily through many layers.
By adding the input of a block back to its output, residual paths help gradients move during training and preserve useful signals.
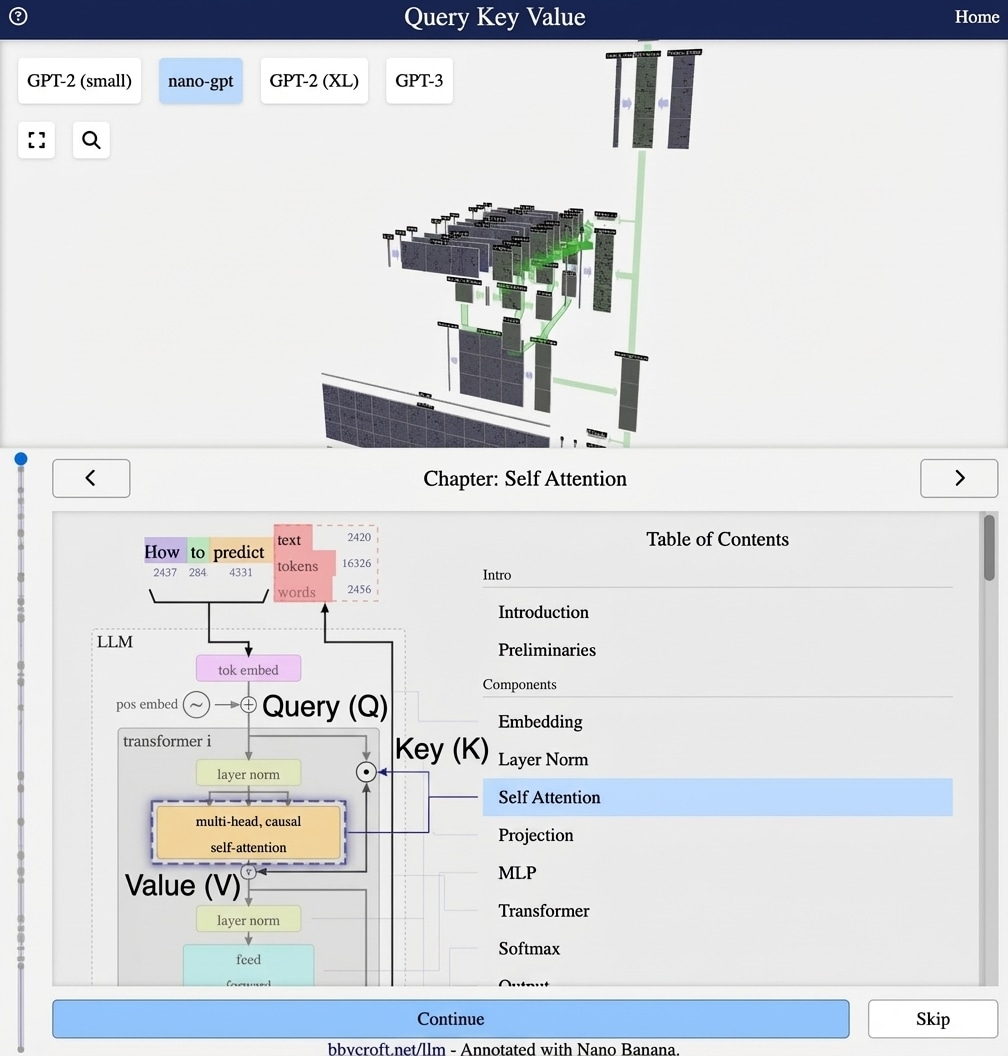
Visualization from bbycroft.net/llm augmented by Nano Banana.
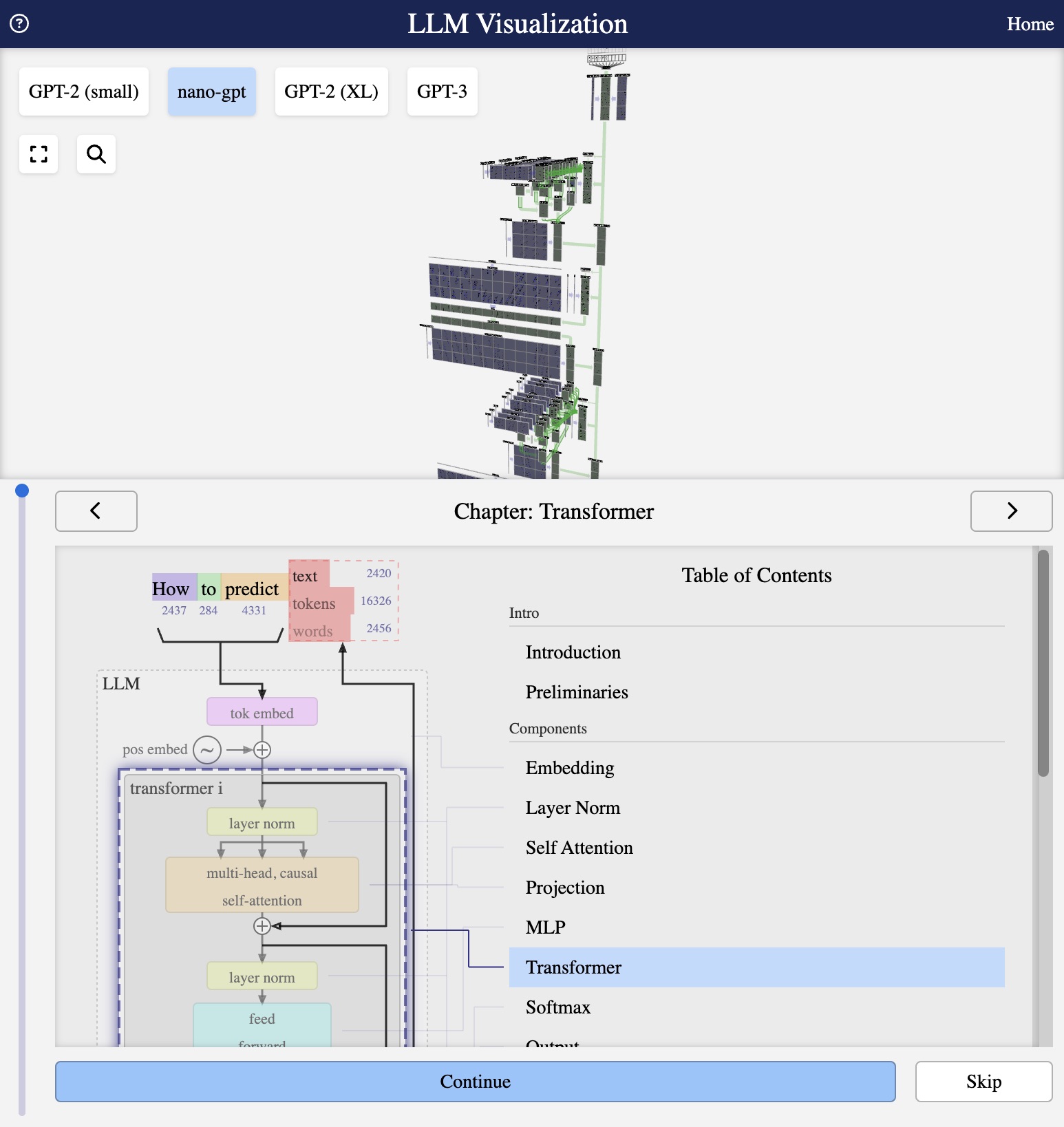
Visualization from bbycroft.net/llm
The Skip Connection
Residual connections (or skip connections) add the input of a layer directly to its output:
output = input + SubLayer(input)
Why Residuals Matter
In deep networks, gradients must flow through many layers. Without residuals:
- Gradients can vanish (become too small)
- Gradients can explode (become too large)
- Deep networks become untrainable
The Gradient Highway
Residual connections create a “gradient highway” – a direct path for gradients to flow from output to input:
∂output/∂input = 1 + ∂SubLayer/∂input
The “1” ensures gradients never completely vanish.
Residuals in Transformers
Each transformer block has two residual connections:
x = x + Attention(LayerNorm(x)) // After attention
x = x + FFN(LayerNorm(x)) // After feed-forwardEnabling Depth
Residual connections are why we can train transformers with 96+ layers. Each layer can focus on learning a small refinement, knowing the original information is preserved.
Series Navigation
Previous: Feed-Forward MLP
Next: The Complete Transformer Block
This article is part of the LLM Architecture Series. Interactive visualizations from bbycroft.net/llm.
Analogy and intuition
Residual connections are like a fast highway that runs in parallel with smaller local roads. Even if some side roads are slow or noisy, the highway keeps traffic moving.
They allow the network to learn corrections on top of an identity mapping, which is much easier than learning a good transformation from scratch.
Looking ahead
Next we will assemble attention, MLP, normalization, and residual paths into a full transformer block.
