The Combined Input Embedding

LLM Architecture Series – Lesson 5 of 20. You have seen token embeddings and position embeddings. Now we put them together into the actual input that flows into the transformer.

This combined embedding is what every later layer sees for each position in the sequence.

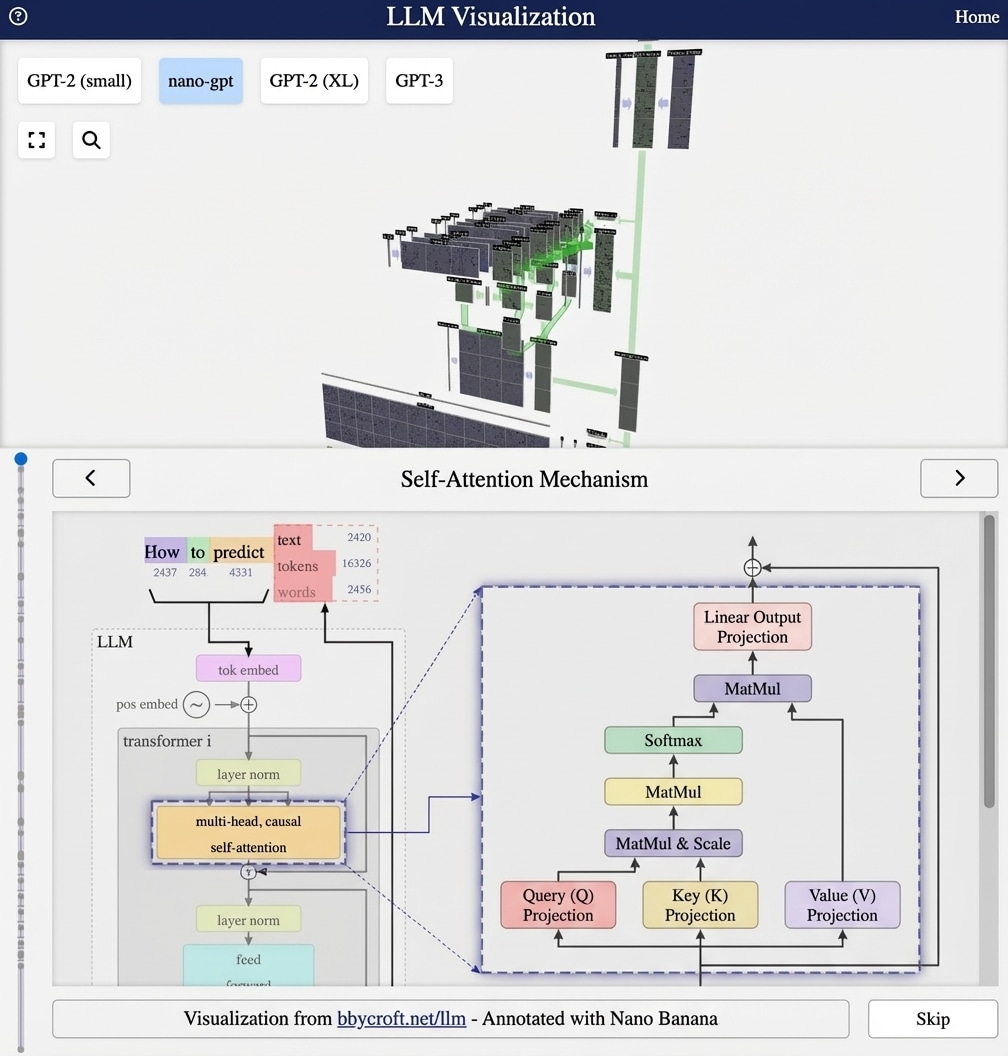
Visualization from bbycroft.net/llm augmented by Nano Banana.

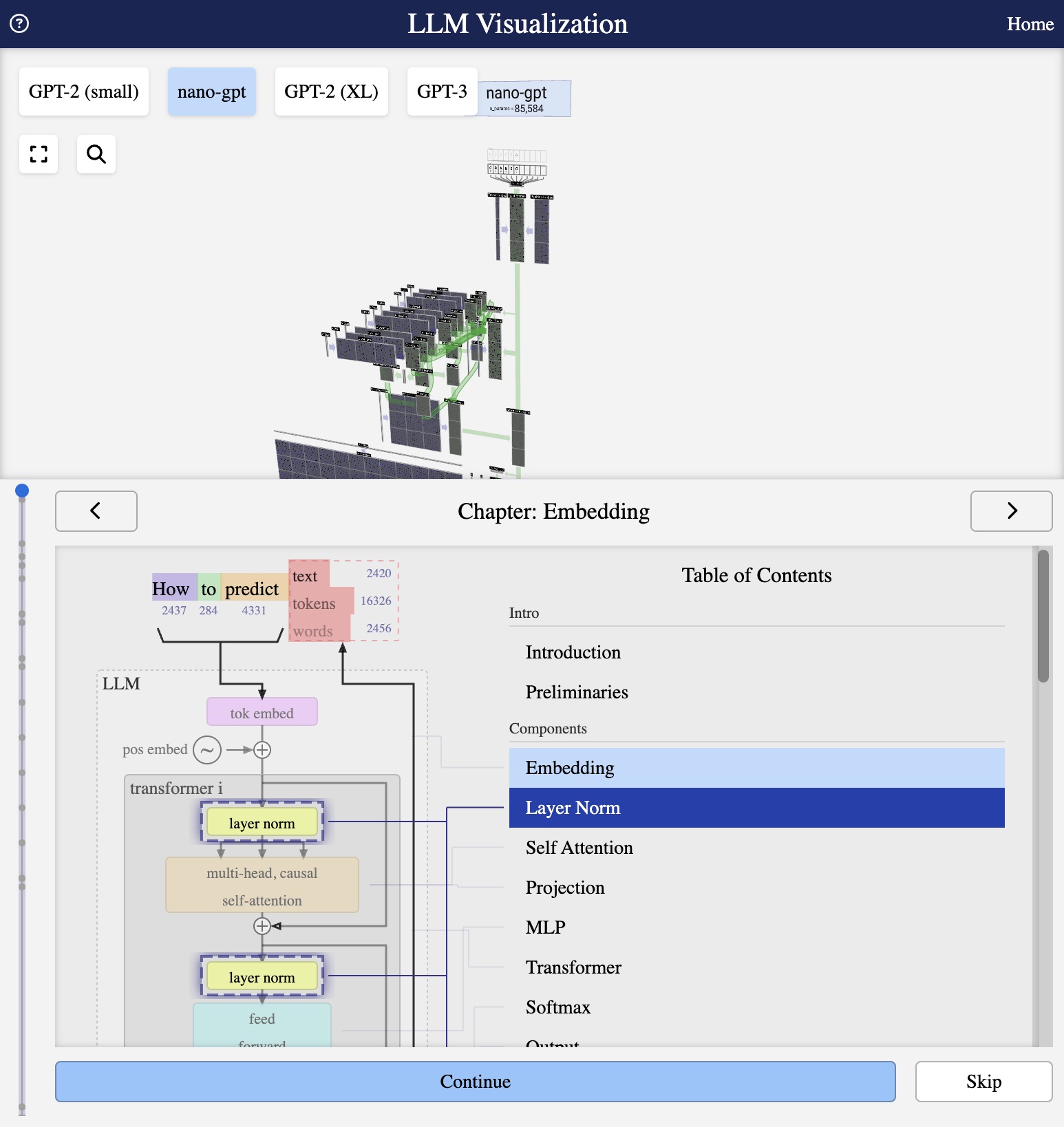
Visualization from bbycroft.net/llm

The Input Embedding Layer

The input embedding is the combination of token embeddings and position embeddings. This combined representation is what actually enters the transformer blocks.

The Complete Formula

For a sequence of tokens [t₀, t₁, …, t_n], the input embedding for position i is:

input_i = E_token[t_i] + E_pos[i]

Dimensions in nano-gpt

For our nano-gpt example with 6 input tokens:

• Token embedding: 6 tokens × 48 dimensions = (6, 48) matrix
• Position embedding: 6 positions × 48 dimensions = (6, 48) matrix
• Combined input: (6, 48) matrix

Why Addition Works

Adding embeddings might seem crude, but it works because:

1. The embedding space is high-dimensional (48+ dimensions)
2. Token and position information can be encoded in orthogonal subspaces
3. The model learns to disentangle them during training

Visualization

In the 3D visualization, you can see:

• Token Embed: Green block converting token indices to vectors
• Position Embed: Separate block for positional information
• Input Embed: The combined result flowing into the transformer

Series Navigation

Previous: Position Embeddings

Next: Layer Normalization in Transformers

---

This article is part of the LLM Architecture Series. Interactive visualizations from bbycroft.net/llm.

Analogy and intuition

You can think of the combined embedding as a playing card that encodes both the value and the suit. The model needs both pieces of information at the same time in order to play correctly.

By adding the two vectors we get a compact way to carry meaning and order together without doubling the dimensionality of the representation.

Looking ahead

Next we will look at layer normalization, a small but important operation that keeps the numbers in a stable range.