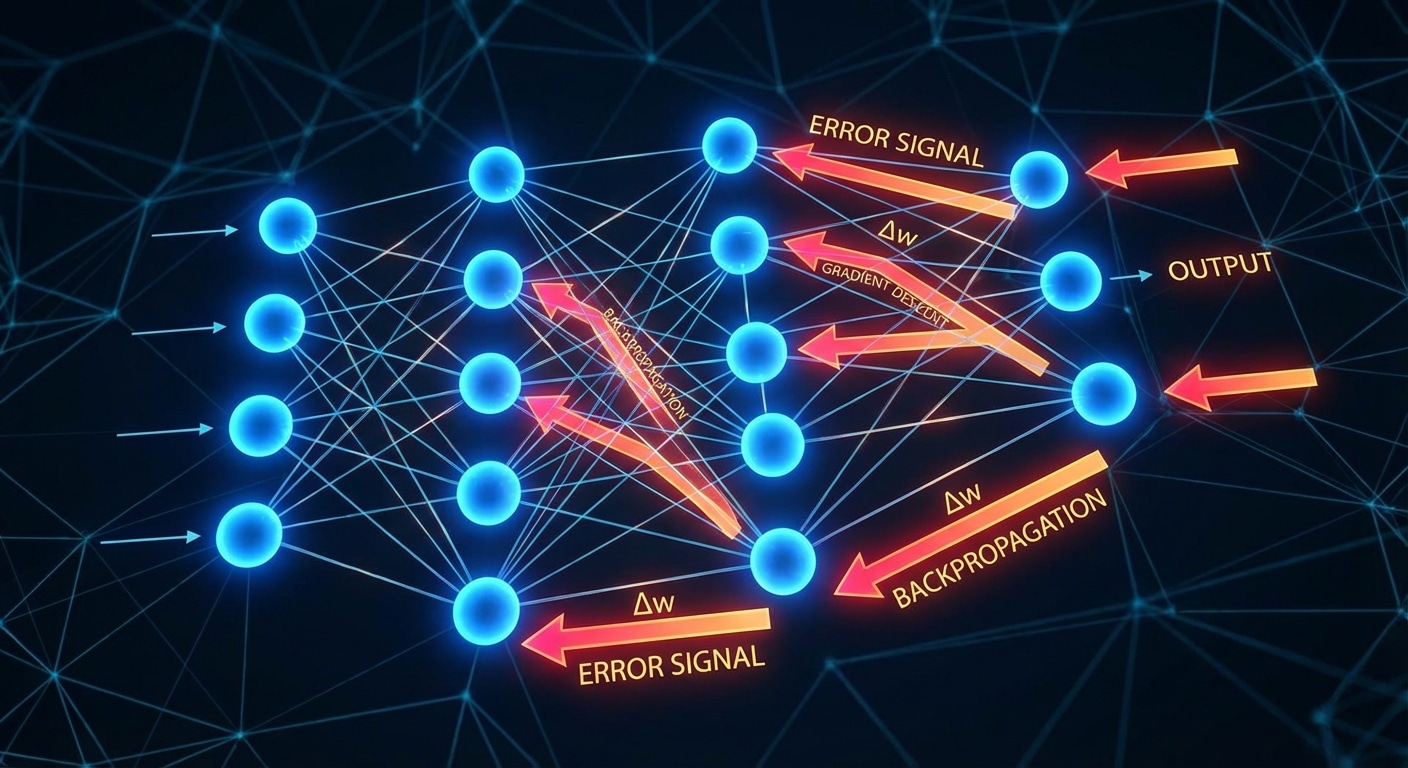
Backpropagation: The Learning Algorithm
Backpropagation is the algorithm that makes deep learning possible. It efficiently computes how much each weight in a neural network contributed to the prediction error, enabling targeted updates that improve performance. Without backprop, training deep networks would be computationally infeasible.
The algorithm applies the calculus chain rule to propagate error gradients backward through the network. Starting from the output layer, it calculates local gradients then multiplies by downstream gradients to determine each weights contribution to the loss. This recursive computation handles arbitrarily deep networks.
The beauty of backpropagation lies in its efficiency. It computes all gradients in a single backward pass through the network, achieving O(n) complexity. Computing each gradient independently would require O(n squared) forward passes, making training prohibitively slow for modern architectures.
Understanding backprop illuminates common training issues. Vanishing gradients occur when gradients shrink exponentially through layers. Exploding gradients cause instability. Techniques like gradient clipping, proper initialization, and batch normalization address these issues while preserving backprops fundamental efficiency.
