Attention Scores and Softmax

LLM Architecture Series – Lesson 11 of 20. We now have raw attention scores between tokens. These scores must be turned into normalized weights.

The softmax over attention scores produces a probability distribution that says how much each token should influence the current position.

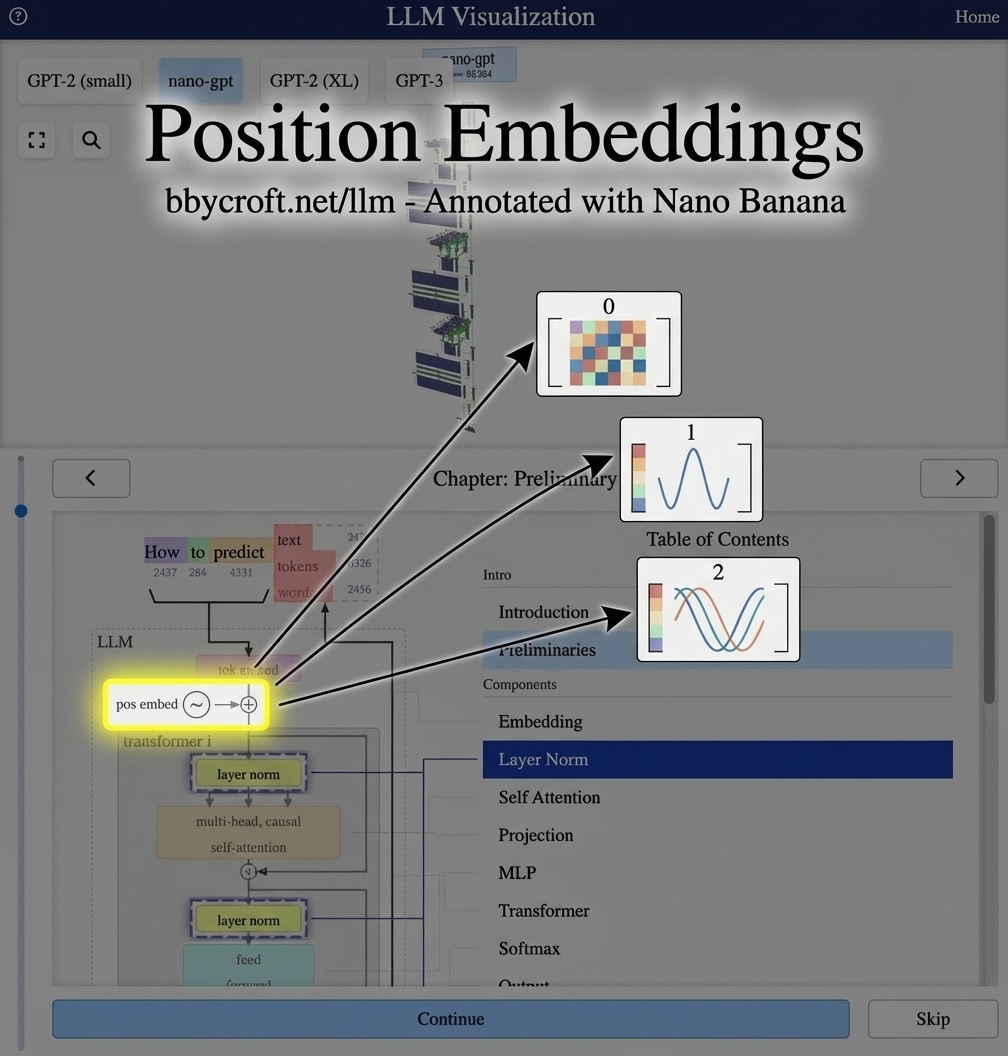
Visualization from bbycroft.net/llm augmented by Nano Banana.

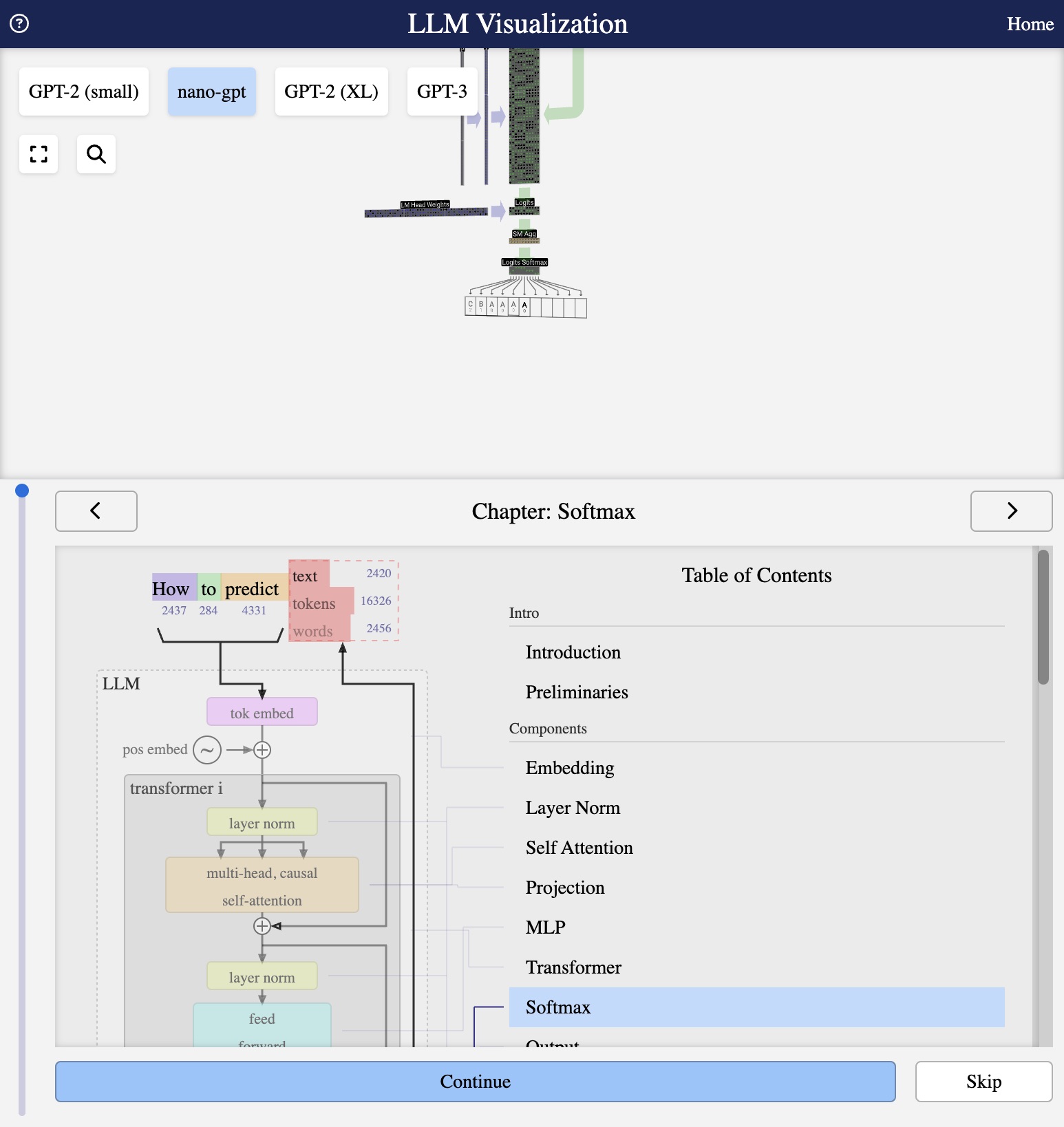
Visualization from bbycroft.net/llm

Converting Scores to Weights

After computing attention scores (QK^T), we need to convert them to weights that sum to 1. This is where softmax comes in.

The Softmax Function

softmax(x_i) = e^x_i / Σ_j e^x_j

Properties:

• All outputs are positive
• Outputs sum to 1
• Larger inputs get exponentially larger weights
• Preserves ranking of inputs

Scaling Factor √d_k

We divide scores by √d_k before softmax. Why?

Without scaling, dot products grow with dimension. Large values push softmax into saturation (outputs near 0 or 1), causing:

• Very small gradients
• Poor learning
• Numerical instability

Attention as Soft Lookup

The softmax attention weights can be viewed as a “soft” version of hard lookup:

• Hard lookup: Pick exactly one item (argmax)
• Soft lookup: Weighted combination of all items (softmax)

This soft approach is differentiable, enabling gradient-based training.

Series Navigation

Previous: Causal Masking

Next: The Projection Layer

---

This article is part of the LLM Architecture Series. Interactive visualizations from bbycroft.net/llm.

Analogy and intuition

Softmax is like taking a list of unscaled votes and turning them into percentages that must add up to one hundred percent.

Very large scores turn into strong attention, while small scores fade almost to zero, which lets the model focus on just a few important tokens.

Looking ahead

Next we will look at the projection layer that converts the combined attention output back into the model hidden dimension.