Causal Masking – Preventing Future Leakage

LLM Architecture Series – Lesson 10 of 20. The attention mechanism is powerful, but for language modeling we must forbid peeking at future tokens.

Causal masking enforces this rule so that the model is always predicting the next token only from tokens that came before.

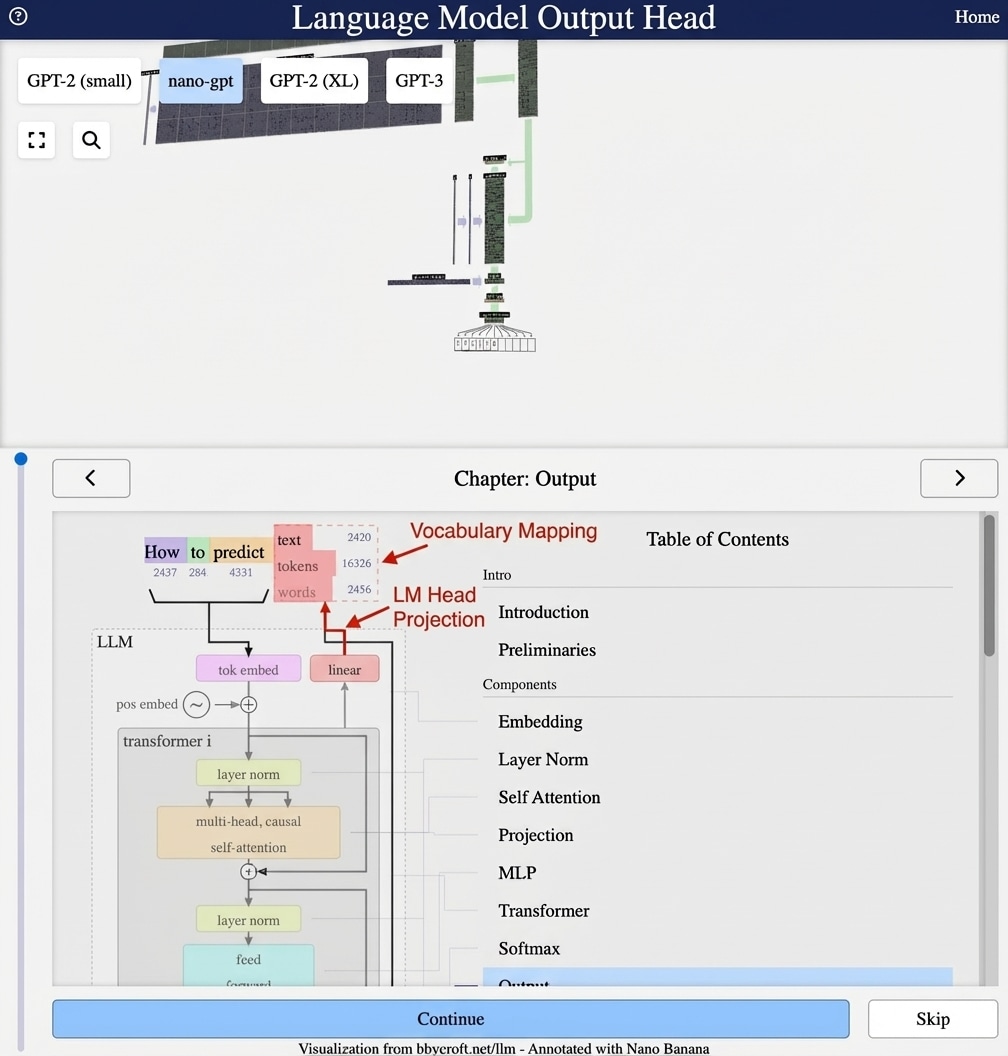
Visualization from bbycroft.net/llm augmented by Nano Banana.

Visualization from bbycroft.net/llm

The Future Leakage Problem

In language modeling, we want to predict the next token given only previous tokens. But standard attention lets each position see all other positions – including future ones!

Causal (Autoregressive) Masking

Causal masking prevents tokens from attending to future positions. Position i can only attend to positions 0, 1, …, i.

Mask[i,j] = 0 if j ≤ i, else -∞

How It Works

Before the softmax, we add the mask to attention scores:

Attention = softmax((QK^T + Mask) / √d_k)V

Adding -∞ to future positions makes their softmax output 0, effectively hiding them.

The Attention Matrix

For a sequence of 4 tokens, the mask creates a lower-triangular pattern:

Position:  0  1  2  3
Token 0:  [1, 0, 0, 0]  (sees only itself)
Token 1:  [1, 1, 0, 0]  (sees 0, 1)
Token 2:  [1, 1, 1, 0]  (sees 0, 1, 2)
Token 3:  [1, 1, 1, 1]  (sees all)

Training Efficiency

Causal masking allows parallel training on all positions simultaneously. Each position learns to predict its successor without seeing the answer – a huge efficiency win over sequential processing.

Series Navigation

Previous: Query, Key, Value

Next: Attention Scores and Softmax

---

This article is part of the LLM Architecture Series. Interactive visualizations from bbycroft.net/llm.

Analogy and intuition

Imagine taking a test where you are only allowed to see the questions you have already answered, not the ones that come later. Causal masking is the rule that hides future questions.

Without this rule, the model could cheat by looking ahead, which would make training easier but inference impossible in an auto regressive setting.

Looking ahead

In the next lesson we examine how attention scores are converted into clean probability weights using the softmax function.